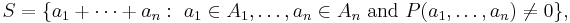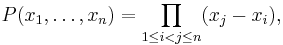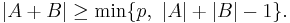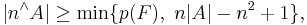Restricted sumset
In additive number theory and combinatorics, a restricted sumset has the form
where  are finite nonempty subsets of a field
are finite nonempty subsets of a field  and
and 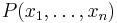 is a polynomial over
is a polynomial over  .
.
When 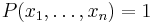 ,
,  is the usual sumset
is the usual sumset  which is denoted by
which is denoted by 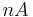 if
if 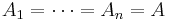 ; when
; when
 is written as
is written as  which is denoted by
which is denoted by 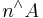 if
if 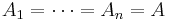 . Note that
. Note that 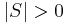 if and only if there exist
if and only if there exist  with
with 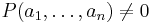 .
.
Contents |
Cauchy-Davenport theorem
The Cauchy–Davenport theorem named after Augustin Louis Cauchy and Harold Davenport asserts that for any prime  and nonempty subsets
and nonempty subsets  and
and  of the field
of the field 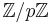 we have the inequality
we have the inequality
Erdős–Heilbronn conjecture
The Erdős–Heilbronn conjecture posed by Paul Erdős and Hans Heilbronn in 1964 states that 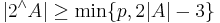 if
if  is a prime and
is a prime and  is a nonempty subset of the field
is a nonempty subset of the field 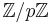 . This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994[1] who showed that
. This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994[1] who showed that
where  is a finite nonempty subset of a field
is a finite nonempty subset of a field  , and
, and 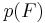 is a prime
is a prime  if
if  is of characteristic
is of characteristic  , and
, and 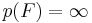 if
if  is of characteristic 0. Various extensions of this result were given by Noga Alon, M. B. Nathanson and I. Ruzsa in 1996,[2] Q. H. Hou and Zhi-Wei Sun in 2002,[3] and G. Karolyi in 2004.[4]
is of characteristic 0. Various extensions of this result were given by Noga Alon, M. B. Nathanson and I. Ruzsa in 1996,[2] Q. H. Hou and Zhi-Wei Sun in 2002,[3] and G. Karolyi in 2004.[4]
Combinatorial Nullstellensatz
A powerful tool in the study of lower bounds for cardinalities of various restricted sumsets is the following fundamental principle: the combinatorial Nullstellensatz.[5] Let  be a polynomial over a field
be a polynomial over a field  . Suppose that the coefficient of the monomial
. Suppose that the coefficient of the monomial  in
in  is nonzero and
is nonzero and  is the total degree of
is the total degree of  . If
. If  are finite subsets of
are finite subsets of  with
with 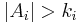 for
for 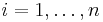 , then there are
, then there are  such that
such that 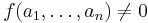 .
.
The method using the combinatorial Nullstellensatz is also called the polynomial method. This tool was rooted in a paper of N. Alon and M. Tarsi in 1989,[6] and developed by Alon, Nathanson and Ruzsa in 1995-1996,[2] and reformulated by Alon in 1999.[5]
References
- ^ Dias da Silva, J. A.; Hamidoune, Y. O. (1994). "Cyclic spaces for Grassman derivatives and additive theory". Bulletin of the London Mathematical Society 26 (2): 140–146. doi:10.1112/blms/26.2.140.
- ^ a b Alon, Noga; Nathanson, Melvyn B.; Ruzsa, Imre (1996). "The polynomial method and restricted sums of congruence classes". Journal of Number Theory 56 (2): 404–417. doi:10.1006/jnth.1996.0029. MR1373563. http://www.math.tau.ac.il/~nogaa/PDFS/anrf3.pdf.
- ^ Hou, Qing-Hu; Sun, Zhi-Wei (2002). "Restricted sums in a field". Acta Arithmetica 102 (3): 239–249. doi:10.4064/aa102-3-3. MR1884717.
- ^ Károlyi, Gyula (2004). "The Erdős–Heilbronn problem in abelian groups". Israel Journal of Mathematics 139: 349–359. doi:10.1007/BF02787556. MR2041798.
- ^ a b Alon, Noga (1999). "Combinatorial Nullstellensatz". Combinatorics, Probability and Computing 8 (1–2): 7–29. doi:10.1017/S0963548398003411. MR1684621. http://www.math.tau.ac.il/~nogaa/PDFS/null2.pdf.
- ^ Alon, Noga; Tarsi, Michael (1989). "A nowhere-zero point in linear mappings". Combinatorica 9 (4): 393–395. doi:10.1007/BF02125351. MR1054015.
External links
- Sun, Zhi-Wei (2006). "An additive theorem and restricted sumsets". Math. Res. Lett. , no. 15 (6): 1263–1276. arXiv:math.CO/0610981.
- Zhi-Wei Sun: On some conjectures of Erdős-Heilbronn, Lev and Snevily (PDF), a survey talk.
- Weisstein, Eric W., "Erdos-Heilbronn Conjecture" from MathWorld.